The 2014 AP CS A Course Description includes 25 multiple choice questions. The questions start on page 23 (according to the PDF file page numbering, not the numbers on the bottoms of the pages). The letter answers are on page 47.
All of the questions are good. Several are fantastic, though some might be too challenging for an actual AP CS A Exam.
Question 1
The loop runs for the even values from 2 up to but not including 20 (0, 2, 4, 6, 8, 10, 12, 14, 16, 18).
The conditional statement evaluates to true for values of k that are 1 more than a multiple of 3. The values 4, 10, and 16 make the condition true and are printed.
Question 2
The diagram below shows the list animals after each step.
After the first 3 calls to add:
animals -> ["dog", "cat", "snake"]
0 1 2
After the call to set:
animals -> ["dog", "cat", "lizard"]
0 1 2
After the last call to add:
animals -> ["dog", "fish", "cat", "lizard"]
0 1 2 3
After the call to remove:
animals -> ["dog", "fish", "cat"]
0 1 2
Question 3
The code segment initially appears to remove all of the zeros from nums. The segment fails to account for the shift when an element is removed, which is a common error.
When the element at position 0 is removed, all subsequent elements shift one position to the left. The code segment increments k every time the loop runs. The code segment will remove one of the two 0 values at the beginning of nums.
The code segment does not go out of bounds, so the only possible answer is D.
See ArrayList practice for related exercises.
Question 4
The code in Case I uses independent if statments, each of which explicitly checks both ends of the desired range. Although silly, this works.
Case II contains code that is syntactically incorrect. The expression 84 <= score <= 92 is not legal in Java.
Case III uses an else if chain to avoid explicitly checking for something that is already known. For example, if the condition score >= 84 is evaluated, score is already known to be < 93. Case III works.
Question 5
This question asks which code segment would produce the given output. The code segments all contain nested for loops. The majority of questions like this feature a single println() call at the bottom of the outer loop. This means that the outer loop controls the number of rows and the inner loop(s) controls what is printed in each row.
Being able to quickly ascertain how many times a for loop runs is an important skill.
The outer loop for each answer choice is the same. It runs 5 times, which is correct.
In choice (A), the inner loop runs 5 times each time the outer loop runs. This would result in 5 values being printed on each line, which does not match the given output.
In choice (B), the inner loop runs 1 time for the first row (when j is 1), 2 times for the second row (when j is 2) and so on. This doesn’t match the given output.
In choice (C), the inner loop runs 5 times for each row. This doesn’t match the given output.
In choice (D), the inner loop runs 5 times for the first row (when j is 1), 4 times for the second row (when j is 2) and so on. This is the correct number of times for each row. The loop prints j, which would result in the given output.
In choice (E), the inner loop runs 5 times for the first row (when j is 1), 4 times for the second row (when j is 2) and so on. Although the number of values output is correct, the loop prints k. This would result in the output below.
1 2 3 4 5
2 3 4 5
3 4 5
4 5
5
Question 6
In object oriented programming, most classes should have state (instance variables) and behavior (methods). In the context of a car dealership, numDoors, hasAir, and milesPerGallon could be appropriate instance variables of a Car class. Methods of Car could use the values of those instance variables when performing tasks such as generating a description. Choice A is correct.
Choice B makes much less sense. If Doors, AirConditioning, and MilesPerGallon are classes, they would have behavior. Although some argument could be made that AirConditioning could have behaviors such as turnOn and setTemperature, these don’t make sense in the context.
Choice C makes even less sense. When a superclass extends a subclass, an “is a” relationship is important. Choice C implies that a Doors is a Car.
Choice D is roughly equivalent to Choice C.
Choice E implies that a Car is a Doors and also that a Car is an AirConditioning.
Question 7
When a class implements an interface, it must have a public method with the same signature as each method from the interface. Only Case I meets the requirement.
It is easy to incorrectly assume that Case II works because a Circle is a Shape. Using the method header from Case II would prevent the isLargerThan method from accepting shapes other than circles.
Case III has both an incorrect parameter type and an incorrect return type.
Question 8
Choice A incorrectly ignores the possibility that adding to minutes could result in one or more additional hours.
Choice B fails to update hours and also updates minutes with the result of a calculation that does not make sense.
Choice C correctly calculates the number of additional hours as minutes / 60. Since both minutes and 60 are of type int, the result will also be of type int. Choice C also correctly calculates the number of remaining minutes as minutes % 60.
Choice D incorrectly switches % and /.
Choice E fails to update minutes to reflect the minutes that were converted into hours.
Question 9
The intent is to advance total, a TimeRecord, for each TimeRecord in timeCards.
Choice A incorrectly runs advance on timeCards[k]. It also fails to pass the required arguments.
Choice B incorrectly runs advance on timeCards[k]. It also fails to pass the required arguments. It also treats advance, a void method, as if it returns a value. It also treats total, a TimeRecord, as if it was a number.
Choice C incorrectly accesses private instance variables of TimeRecord in a class other than TimeRecord.
Choice D correctly runs advance on total and with correct arguments. Choice D correctly runs public methods of TimeRecord to access the hours and minutes of timeCards[k].
Choice E incorrectly runs advance on timeCards[k]
Question 10
The mystery method implements a variant of binary search. My binary search page references this specific question under the Binary search with insertion point return variant.
When num is found in arr, mystery returns the position of num in arr, as usual. When num is not found in arr, this variant returns where num would go if it was to be inserted into arr (and the sorted order maintained).
What makes this question so challenging is that none of the answer choices initially appear to have anything to do with what this method does. Solving the problem requires careful consideration of the precondition.
“the elements in arr are in ascending order” is a standard precondition for binary search. “arr contains no duplicates” is not a standard precondition for binary search. If arr does not contain duplicates, the position of num in arr is equivalent to the number of elements that are less than num.
Consider the example below.
arr -> [10 15 17 20 25 30]
0 1 2 3 4 5
mystery(0, 5, 20) returns 3 (the position of 20 in arr). There are 3 elements less than 20.
The assertion in answer choice (A) holds even if num is not in arr.
mystery(0, 5, 22) returns 4 (the position at which 22 would go in arr). There are 4 elements less than 22.
There is nothing special about the first or last values in arr, nor values that would be inserted after the first or last values.
Question 11
Method findLongest fails to set lenCount back to 0 at the end of each run. lenCount is incremented every time val == target.
The condition lenCount > maxLen is checked at the end of each run and after the loop. Since lenCount only goes up, maxLen will end up as lenCount.
findLongest returns the number of times target is in nums (choice C).
Question 12 provides a strong hint for Question 11 if the error in findLongest is not obvious.
For additional information see Finding the minimum or maximum and the Run length increasing exercise.
Question 12
As discussed in the Question 11 explanation, findLongest fails to set lenCount back to 0 at the end of each run of target. lenCount must be set back to 0 at the end of each run, after maxLen has been updated if necessary. Choice E updates lenCount in the necessary location.
Choice A incorrectly sets lenCount to 0 each time the loop runs. This prevents counting the number of consecutive occurrences of target.
Choice B incorrectly sets lenCount to 0 before the check to see if the current run is longer than the longest run so far. This prevents updating maxLen.
Choice C incorrectly sets lenCount to 0 before actually updating maxLen.
Choice D incorrectly sets lenCount to 0 only if the length of the current run is the new maximum.
Question 13
The loop runs backwards through numbers. The first time it finds a value < num, it stops and returns the index of that value.
Every value for which the condition evaluated to false is >= num. Those are the values after the returned index. This is what choice C states.
Question 14
When I see a print statement in a recursive method on an Exam, I get excited. print statements often make recursion problems way easier to solve.
See Recursive methods with print statements for an explanation of the approach.
Answer choice (E) mentions infinite recursion. My preference is to handle that answer choice first. To determine if the method call mystery(1234) results in infinite recursion, consider the base case and the recursive call.
The recursive call is inside an if statement so the base case is the opposite of the condition. The base case is x / 10 == 0. x / 10 removes the last (rightmost) digit of x. The base case is when a digit is removed and the result is 0.
The recursive call is mystery(x / 10). The method is called with x without its last digit.
Repeatedly removing the last digit of x will eventually result in 0, so the method is not infinitely recursive.
mystery contains 2 print statements, each of which prints x % 10, the last (rightmost) digit of x. One print statement is before the recursive call. The other print statement is after the call. The value of x is not changed within mystery.
The first and last values that will ever be printed are both 4. Only answer choice (D) includes 4 as the first and last digit.
This question is not an exception. It is very common for questions that include recursive methods with print statements to be easily solved by considering the position of the print statement(s) relative to the recursive call(s).
Question 15
Although this question does not include an answer choice that indicates that the act method cannot be run, I encourage my students to apply the first rule of polymorphism anyway.
The first rule of polymorphism is: The variable/reference type determines what methods CAN BE run.
fido.act() is a legal call because act is in Dog. If act was not in Dog, the call would not be legal, regardless of whether act was in UnderDog.
The second rule of polymorphism is: The object/instance type determines what method IS ACTUALLY run (and the most specific method possible is run).
The initial call to fido.act() runs the act method from UnderDog because the actual object type is UnderDog.
The initial call results in additional method calls. Once it becomes obvious that keeping track of a potentially complex sequence of method call is required, a stack based trace should be used. None of these method calls are recursive, but stack based tracing is appropriate for keeping track of any complex sequence of method calls.
The trace below shows the stack at each step as well as everything that has been printed so far, and an explanation of the changes from the previous step.
Step 1
UnderDog's act()
The initial call is to the act method of UnderDog.
Step 2
Dog's act()
UnderDog's act()
super.act() calls the act method of Dog.
Step 3
UnderDog's eat()
Dog's act()
UnderDog's act()
printed:
run
The act method of Dog prints "run" then calls eat. The call to eat runs the eat method of UnderDog. This is very commonly misunderstood. Both rules of polymorphism apply here.
eat is a legal call because the eat method is in Dog. If the eat method was not in Dog, the call would be a compile time error.
The actual object type is UnderDog, which means the eat method from UnderDog is run. This is true even though the eat method call is within a method of Dog.
Step 4
Dog's eat()
UnderDog's eat()
Dog's act()
UnderDog's act()
printed:
run
super.eat() calls the eat method of Dog.
Step 5
Dog's eat() returns
UnderDog's eat()
Dog's act()
UnderDog's act()
printed:
run eat
The eat method of Dog prints "eat" then returns. Control returns to UnderDog's eat().
Step 6
Dog's eat() returns
UnderDog's eat() returns
Dog's act()
UnderDog's act()
printed:
run eat bark
The eat method of UnderDog prints "bark" then returns. Control returns to Dog's act().
Step 7
Dog's eat() returns
UnderDog's eat() returns
Dog's act() returns
UnderDog's act()
printed:
run eat bark
The act method of Dog returns. Control returns to UnderDog's act().
Step 8
Dog's eat() returns
UnderDog's eat() returns
Dog's act() returns
UnderDog's act() returns
printed:
run eat bark sleep
The act method of UnderDog prints "sleep" then returns. Control returns to the method that made the initial call. (We’re done.)
Question 16
The method is called with a power of 2.
The base case is when n <= 1, in which case mystery returns 0.
The recursive call is with n / 2.
Each time the method runs, it adds 1 to the result. The method is counting how many times it runs.
The method divides n by 2 each time it runs and stops when n <= 1. The return value is equivalent to how many times n be divided by 2. Since n is a power of 2, the method returns the power (choice B).
See Recursive method analysis for an explanation of the technique.
Question 17
With the exception of the initial value of loc, this is a standard find the max. loc is used as an index throughout the code, so the method returns the index of the maximum (choice D).
When finding the min/max, it is typical to start the min/max at the first value that could be the min/max. This isn’t actually required. It is possible to start at any value that could be the min/max as long as all possible values are checked. In some cases, it is also possible to start at other values. See Find the minimum or maximum for details.
Question 18
All arguments in Java are passed by value. When a method is called with arguments, a copy of each argument is used to set the value of each parameter. A variable of primitive type stores its value directly. A variable of class type stores the memory address of an object (or null).
See Primitive types vs references exercises for a detailed demonstration of variable types. See Primitive types vs references exercises with calls for detailed examples of passing arguments to methods.
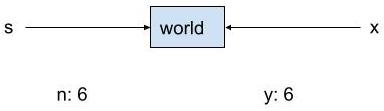
In test before the call to changer, the value of s is the memory address of "world". The value of n is 6.
The call changer(s, n) passes copies of the values of s and n to changer. x is set to the memory address of the same String as s. y is set to 6. The diagram below shows the state immediately after the call to changer.
String objects are immutable. The statement x = x + "peace"; makes a new String containing "worldpeace" and changes the value of x to the memory address of the new String. The value of s remains unchanged.
The statement y = y * 2; changes the value of y. The value of n remains unchanged.
When changer ends, x and y go away. The value of s, the value of n, and the state of the String to which s points are all unchanged.
Question 19
mat is created with 3 rows and 4 columns.
Choices A and B have the number of rows and columns reversed.
The loops visit each value in mat (in row major order).
Positions for which row < col are set to 1. These positions are from the top right corner to the top left to bottom right diagonal.
Positions for which row == col are set to 2. These positions are the top left to bottom right diagonal.
Remaining positions are set to 3.
This corresponds to choice D.
This problem can also be solved by evaluating the values for the first row.
See Intro to 2D arrays for additional discussion.
Question 20
This question is a clever variation of finding the maximum.
The loop runs while the index (k) is valid and while the current element is less than lim, a parameter. The conditional statement and the code inside are part of the standard algorithm for finding a maximum. (If the current element is greater than the maximum so far, update the maximum.)
The question asks which combinations of lim and the number of executions of the labeled statements is/are valid.
v stores the value of the maximum. It is initialized to 0.
/* Statement S */ executes each time a new maximum is found and v is updated.
/* Statement T */ executes each time the loop runs.
The value of lim is not relevant for any of the cases.
In Case I, the loop runs 5 times but v is never updated. Although this would normally be possible (if all the elements were less than or equal to 0), the precondition is “arr contains only positive values”. If the loop runs 5 times, v must be updated at least once.
Case II is fine. The loop runs 9 times and v is updated 4 times.
Case III is clearly incorrect. v cannot be updated more times than the loop runs.
Question 21
Implementation 1 starts j at 0 and accesses sum[j - 1]. This results in an ArrayIndexOutOfBoundsException on the first loop execution.
Implementation 2 explicitly computes each partial sum by visting the elements in arr from 0 up to and including j for each position j in sum. The outer loop actually loops through sum, not arr, despite the condition.
If it worked, Implementation 1 would more efficiently compute each partial sum by adding arr[j] to the previous partial sum. Two modifications are required for Implementation 1 to work. j must start at 1 and sum[0] must be set to arr[0] before the loop.
Question 22
Case I is legal. Every subclass constructor must call a superclass constructor, either explicitly or implicitly. In this case, NamedPoint() does not explicitly call a superclass constructor. The call super() is implicitly (automatically) made as the first line. Class Point has a constructor that takes no parameters, so this works.
Case II incorrectly accesses private instance variables from the superclass.
Case III correctly calls the Point constructor that accepts 2 int parameters. The explicit call to the superclass constructor is correctly the first line in the subclass constructor.
See Inheritance and polymorphism for more details.
Question 23
n is the length of both nums and result. The loop runs through each value from 0 up to but not including n / 2. Each time the loop runs, it accesses 2 elements from nums and copies them to 2 positions in result.
Assuming the 2 lines in the loop body do whey they appear to do, this approach will fail when n is odd. If the loop ran up to and including n / 2, the code would go out of bounds at the end. Since n / 2 is not included, the loop skips the last element.
In Example 1, n is 8, which is even. The loop runs when j is 0, 1, 2, and 3.
j |
j + n / 2 |
j * 2 |
j * 2 + 1 |
|---|---|---|---|
0 |
4 |
0 |
1 |
1 |
5 |
2 |
3 |
2 |
6 |
4 |
5 |
3 |
7 |
6 |
7 |
In Example 2, n is 7, which is odd. The loop runs when j is 0, 1, and 2.
j |
j + n / 2 |
j * 2 |
j * 2 + 1 |
|---|---|---|---|
0 |
3 |
0 |
1 |
1 |
4 |
2 |
3 |
2 |
5 |
4 |
5 |
Question 24
Case I correctly treats the 2D array m as an array of 1D arrays. It passes a reference to each row in m to method sum1D and sums the result.
Case II does the same thing as Case I, except it uses an enhanced for loop.
Case III uses a pair of enhanced for loops, which also works.
See Treating a 2D array as an array of 1D arrays and Enhanced for loop exercises for additional discussion, memory diagrams, and practice.
Question 25
The algorithm is a standard implementation of selection sort. See Selection sort for a detailed discussion of the algorithm.
Case I modifies the conditional statement such that it finds the maximum instead of the minimum. If the maximum is repeatedly swapped with the first element in the unchecked part, the array would be sorted in descending order.
Case II modifies which array value is stored in temp for the swap. This has no effect on the algorithm’s behavior.
Case III modifies the outer loop to traverse the array backwards. It also modifies the inner loop to traverse the left side of the array. Each minimum is swapped to the end of the array, which results in the array being sorted in descending order. The modification to the inner loop is important. The inner loop must traverse the unchecked part of the array, which would be on the left (since the outer loop goes backwards).